How To Determine The Order Of Differential Equation And Its Degree?
Order of Differential Equation
The number of the highest derivative in a differential equation.
A differential equation of order 1 is called first order, order 2 second order, etc.
Example: The differential equation 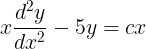 is second order since the highest derivative is
is second order since the highest derivative is 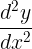 or the second derivative.
or the second derivative.
The Differential equation  is first order since the highest derivative is
is first order since the highest derivative is 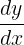 or first derivatives only.
or first derivatives only.
The Differential equation is third order since the highest derivative is
or third order derivatives only.
So the first concept is clear that the number of times the derivative of the function is taken is the Order of that differential equation
Lets move to the secon part that is Degree of the Differential Equation
Degree of Differential Equation
The Highest power of Highest order derivative in a differential equation is called the Degree of differential equation.
This definition has one key point that if overlooked can result in wrong answers, i.e. You must look for the highest power of highest order derivative and not every derivative,
Let us see the example below
Here the highest order = 3
and highest degree is ????? 3.....No it is wrong ...Because power 3 doesnot belongs to the highest order derivative in the equation, so it is not the degree of the equation,but actual degree of equation is 1. Why so ? Because the highest power of the third order (Highest order) Derivative is 1.
Answer is : Order:3 Degree:1
Let us try some more examples
ORDER = 3 and Degree=1 { Here 2 is not degree although it is highest in the equation because it does not belongs to highest order derivative..
Watch the videos below to get more clear idea and how to solve the examples....